画家としてのTransfomer レイヤー: Transformer Layers as Painters
Qi Sun 著 · 12 Feb 2025 · Emergence AI・Sakana AI・Institute of Science Tokyo
Focus
学習済みTransformerモデルのレイヤーに対し、削除、並べ替え、並列化などの操作を行う実験構成

Keyword
ARC:AI2 Reasoning Challenge
複雑な推論能力を評価するベンチマーク
- 特に段階的な思考プロセスが要求される問題を含む
- レイヤーの処理順序に対する感応性が高いことが実験的に示された
HellaSwag:
常識に基づく推論と文脈補完能力を測るベンチマーク
- 意味内容の理解が主であり、レイヤー順序の変更に対して比較的ロバスト
GSM8K:Grade School Math 8K
算数の文章問題解決能力を測るベンチマーク
- 特に正確な計算手順の実行能力を評価
- レイヤーの処理順序が算術演算の正確性に影響を与える可能性を示唆
Wino-Grande:
代名詞の指示対象を文脈から正しく特定する能力を測るベンチマーク
- 従来からあるWinograd Schema Challenge (WSC) を発展させた、より大規模で、難易度の高い問題
LAMBADA:
広範な文脈理解に基づいた、次に来る単語の予測能力(語彙的連鎖)を測るベンチマーク
- モデルの基本的な言語理解能力を評価する指標の一つ
Switch Transformers
MoE(Mixture-of-Experts)とスパースな活性化を活用することで、LLMの持つ潜在能力を最大限に引き出しながら、実際の計算コストを抑制するアプローチ
- スパースな活性化
- MoEアーキテクチャの採用し、入力ごとにごく一部のパラメータ(エキスパート)だけを使用する
- ルーティング機構の簡素化
- トークンごとにどのエキスパートを利用するかを決めるルーティングのアルゴリズムが簡潔に設計されている
- 従来の複雑なMoEシステムよりも扱いやすく、訓練が容易
- スケーラビリティ
- エキスパートの数を増やすことで、モデル全体のパラメータ数を劇的に増加させる
- 実際に計算する際はごく一部のみが稼働させるため、実用的な計算コストでスケールアップを実現可能
Overview
WHAT(これは何?)
学習済みTransformerモデルのレイヤーが、削除、並べ替え、並列化などの操作に対してどの程度の頑健性を持ち、効率化の余地があるかを示した
WHY(論文の価値は?)
- 様々な実験を通じて、Transformerモデルの内部構造に対する新たな理解を提供
- 学習済みモデルのロバスト性に関する洞察
- 問:実験は、全般的に緩やかな性能低下を示したが、なぜ層が摂動のほとんどに対してある程度の頑健性を持つのか?
- 一つの仮説:訓練中の残差接続がレイヤー間で共通の表現を共有するために必要なのではないか
- 将来的なTransformerアーキテクチャの改善に向けた方向性を示唆
- FutureWork:関連研究との比較を通じて、Transformerレイヤーに関する理解を深める
- モデルを「解凍」し、Transformerが微調整を通じて本論文のバリアントに適応するかどうかを調査する予定
- 並列化とスキップの両方がフルモデルよりも潜在的に低いレイテンシを持つことに注目
- 例:
- N=8のLlama2-7Bの並列レイヤーのレイテンシは、通常のLlama2-7Bの約半分になるはず
- 既存の学習済みモデルのより効率的な利用方法を示唆
- 精度とレイテンシのトレードオフを容易に行う単純な方法
- Switch Transformersのように、凍結レイヤーを実行するためのルーティングメカニズムを通常のモデルにも適用できるのではないか
- 実験により、全てのレイヤーを常に順番通りに実行する必要はないことが示されたため
- 多数の層の中から、入力された情報に応じて、一部の必要な層だけを選んで処理を行う
ルーティングメカニズム
WHERE(調査のキモはどこ?)
学習済みTransformerの内部レイヤーの動作と、その構造を変更した場合のモデルの挙動を知るため、ユニークな実験を実施した
- レイヤー間の情報の流れと表現の共有性
異なる層が同じ表現空間を持つか
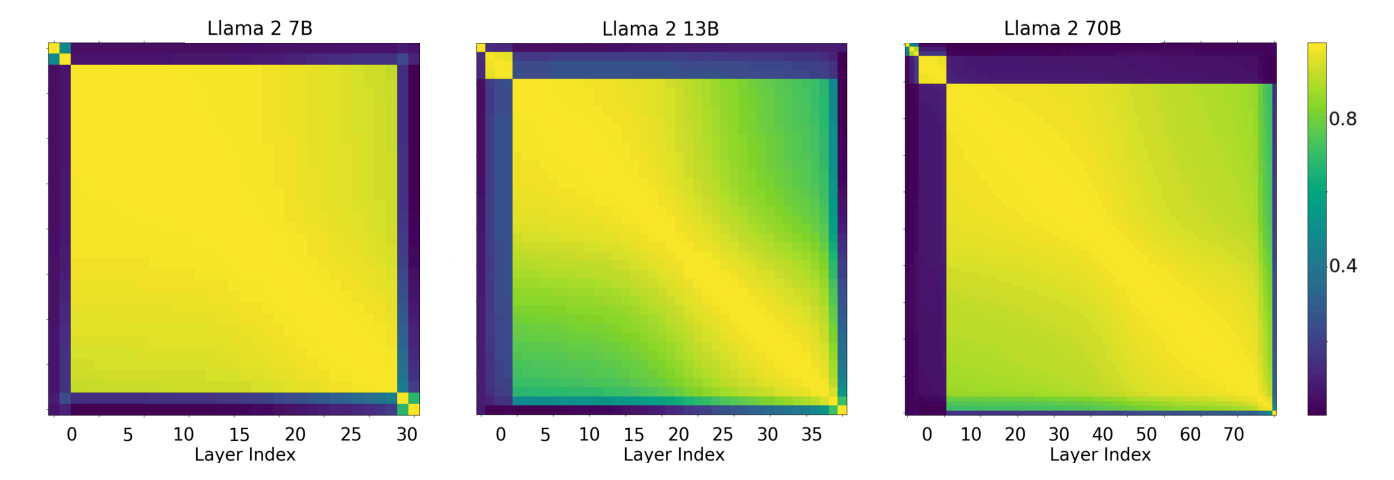
Do Layers “Speak the Same Language”?
実験方法
- 特定の層をスキップする、隣接する層の順序を入れ替える
- Llama2-7Bのスキップ例:
- 層4の出力を層6へ入力する
- 通常、層6は層5からの出力を想定している
- 異なる層の隠れ状態の活性化間の平均コサイン類似度をベンチマーク全体で測定した
結果
- 初期層のスキップはパフォーマンスに破滅的な影響をもたらす
- 中間層のスキップのパフォーマンスは通常のベースラインとほぼ同じ

- モデルは「開始」、「中間」、「終了」層に対して3つの異なる表現空間を持っている
- 開始層と中間層は、総層数に比例して増加する
- 終了層は1-2に固定されている
- 中間層の特性
- 表現空間を共有している
- 「外側」(最初と最後の数層)の層とは異なる表現空間を持っている
Llama2-7B(全32層)、Llama2-13B(全40層)、Llama2-70B(80層)のコサイン類似度
- 個々のレイヤーの必要性
全ての層が必要か
Are All the Layers Necessary?
実験方法
- 層のスキップ
- 例:
- N番目の層の出力を層N + M(M>1)の入力に直接送ることで、M - 1層をスキップ
- 通常、層N + Mは本来層N+M-1からの入力でのみ訓練されている

- 層N + Mが層Nからの活性化を理解できるかどうかを確認する
結果
- スキップする層数が増えるにつれ、緩やかにパフォーマンスが下がる
- 全ての層を保持しなくても良い

- fine-tuning
- 少数の層をスキップする場合は、fine-tuningでパフォーマンス向上するが、多くの層をスキップするとfine-tuningでパフォーマンスが落ちる
中間層は全て同じ処理をしているか
Are Middle Layers All Doing the Same Thing?
実験方法
- 中間層の一定区間を、最も中央の層の同数のコピーで置き換える
- 中間層をT − 2N + 1回繰り返す

結果
- 中間層を完全にスキップするよりも、中央層の重みで置き換えた方が性能が大幅に低下する

- 中間層を繰り返すことで、共有していた表現空間から外れてしまう

スキップのヒートマップ(左)が元のLlama2-7Bモデルと同じコサイン類似度の傾向を示している一方、中間繰り返しヒートマップ(右)では、繰り返された中央層によって隠れ状態が互いにかけ離れていく
- 中間層は表現空間を共有しているものの、その空間上で異なる演算を実行していると考えられる
- レイヤーの順序の重要性
層の順序は重要か
Does the Layer Order Matter?
実験方法
- 訓練時と逆順で中間層を実行
- 層T-Nの出力をT-N-1の入力に送り、この層の出力をT-N-2に送る(逆順)。これを層Nまで続け、その後この層の出力を最後のT-N層に送る

- 中間層をランダムな順序に入れ替えて実行(結果は10個のランダムシードで平均化)
結果
- 層のスキップよりも緩やかにパフォーマンスが低下する

- 層は、訓練時とは異なる入力源(つまり、異なる層)から入力を受けた場合でも、依然として貢献できると考えられる
- 層の順序はある程度重要である。
- 中間層の順序をランダム化しても逆転しても、緩やかな性能低下に留まる
- ランダム順の方が逆順よりも良い性能を示している
- 考察:
- どんなランダムな順序でも、完全な逆順に比べて、少なくとも同程度の一貫性(層iが層jの後にある場合、i > j)を持つからではないか
- レイヤーの並列実行の可能性
層を並列に実行できるか
Can We Run the Layers in Parallel?
実験方法
- 層NからT-Nをスキップする代わりに、中間層を並列に実行し、その平均結果を最後のN層に送る(T: 総層数)
- 初期の入力から層を独立して実行し、その結果をマージできるかどうか

結果
- GSM8Kの数学的文章題を除くベンチマークで緩やかなパフォーマンス低下を示した

- ここまでの実験のパフォーマンス(高い順)
- ランダム化 > 逆順実行 > 並列化 > スキップ
- 特定のタスクにおけるレイヤー順序の影響
タスクによって順序の重要性は異なるか
Does the Order Matter for Some Tasks More Than Others?
考察
- ここまでの実験より、抽象的な推論(ARC)や数学的な推論(GSM8K)のベンチマークは、逆順実行・スキップ・並列実行を含むほとんどの変形において、最も急激な性能低下を示した
結果
- 推論タスクは、WinograndeやHellaSwag(常識)のような意味的タスクに比べて、層の順序により敏感になる
- 推論には構造と意味の両方が必要である
- 常識的タスクは意味だけで十分
- 数学的タスクと推論タスクは、意味的 semantic タスクよりも順序依存性が高い
- 例:
- 3セットの衣服の総費用を尋ねる質問
- Llama2-7B(N = 14)の並列バリアントは、正しい計算式を設定したが、その実行において誤りを犯した

並列化した層のループは効果があるか
Does Looping Help Parallelized Layers?
実験方法
- 並列化した層の平均出力を同じ層に一定回数フィードバックする実験

- 異なる反復回数で同じ実験を繰り返す
結果
- 並列化した層を3回ループさせた結果、3回ループは1回のループと比べて大きく改善した

- 最適な反復回数は並列化した層の数にほぼ比例する

もっとも害が少ないのはどのバリアントか
Which Variants Are Least Harmful?
考察
- 実験における異なるバリアントをすべて1つのプロットで比較
- 全ベンチマークにおけるLlama2の中央値またはBERTの平均値をプロット

結果
- 中間層の繰り返しは最も急激な性能低下を示した
- 急速にランダムなベースライン性能まで低下
- ループ並列と層のランダム順序は最も緩やかな性能低下を示した
- ループ並列がBERTとLlama2-7Bの両方で最良のバリアント
